Mesa de Análisis de Datos in situ: Aprendizaje automático para datos espaciales
Mariano Córdoba, Pablo Paccioretti, Mónica Balzarini
Octubre, 2022
Interpolación Kriging
Kriging es considerado como el método de referencia para el análisis de datos geoestadísticos.
Toma un modelo estadístico integral como punto de partida y deriva en una predicción óptima.
Explota la autocorrelación espacial en la variable de interés.
Proporciona una medida espacialmente explícita de la incertidumbre de la predicción.
Interpolación Kriging
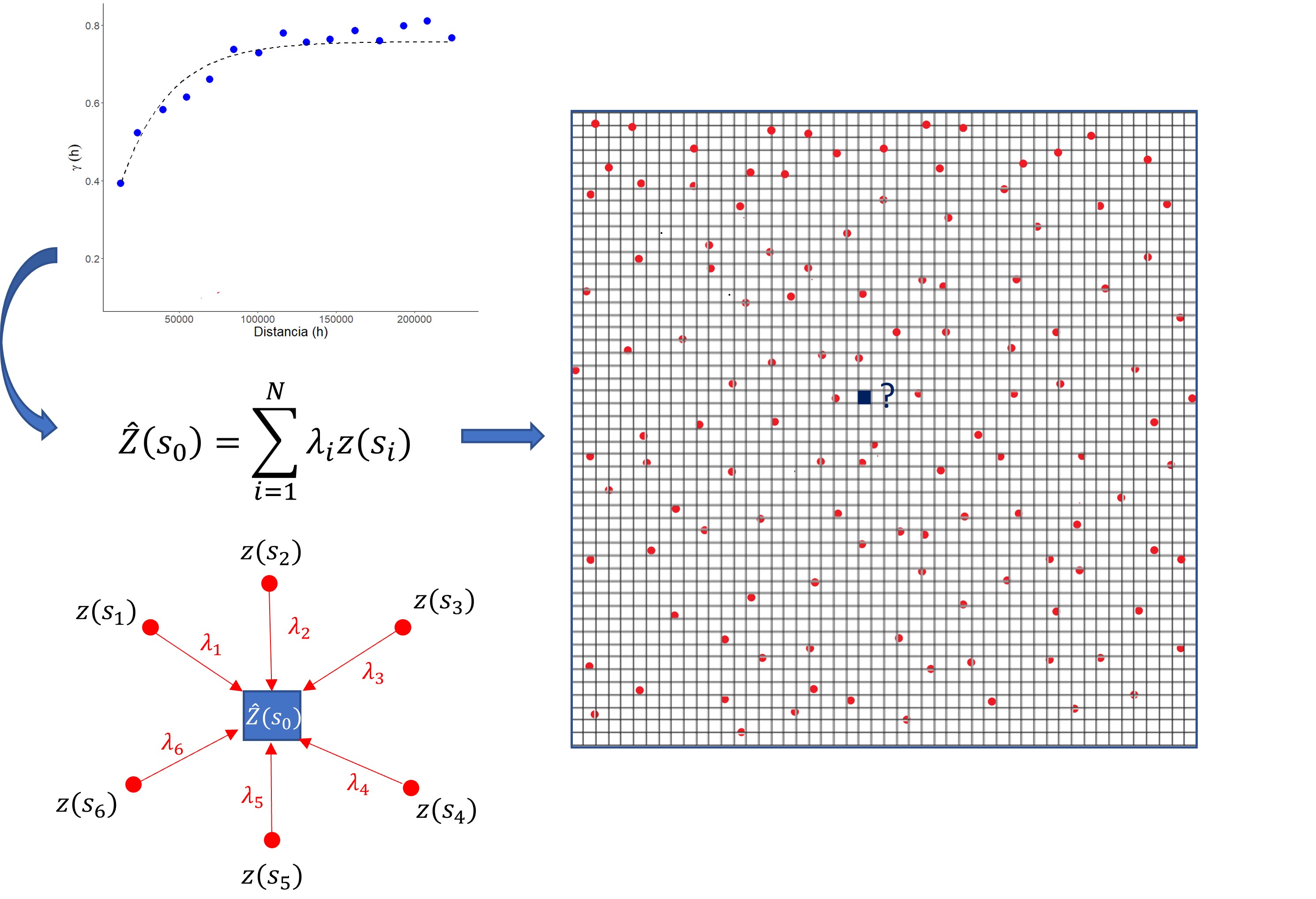
Interpolación Kriging
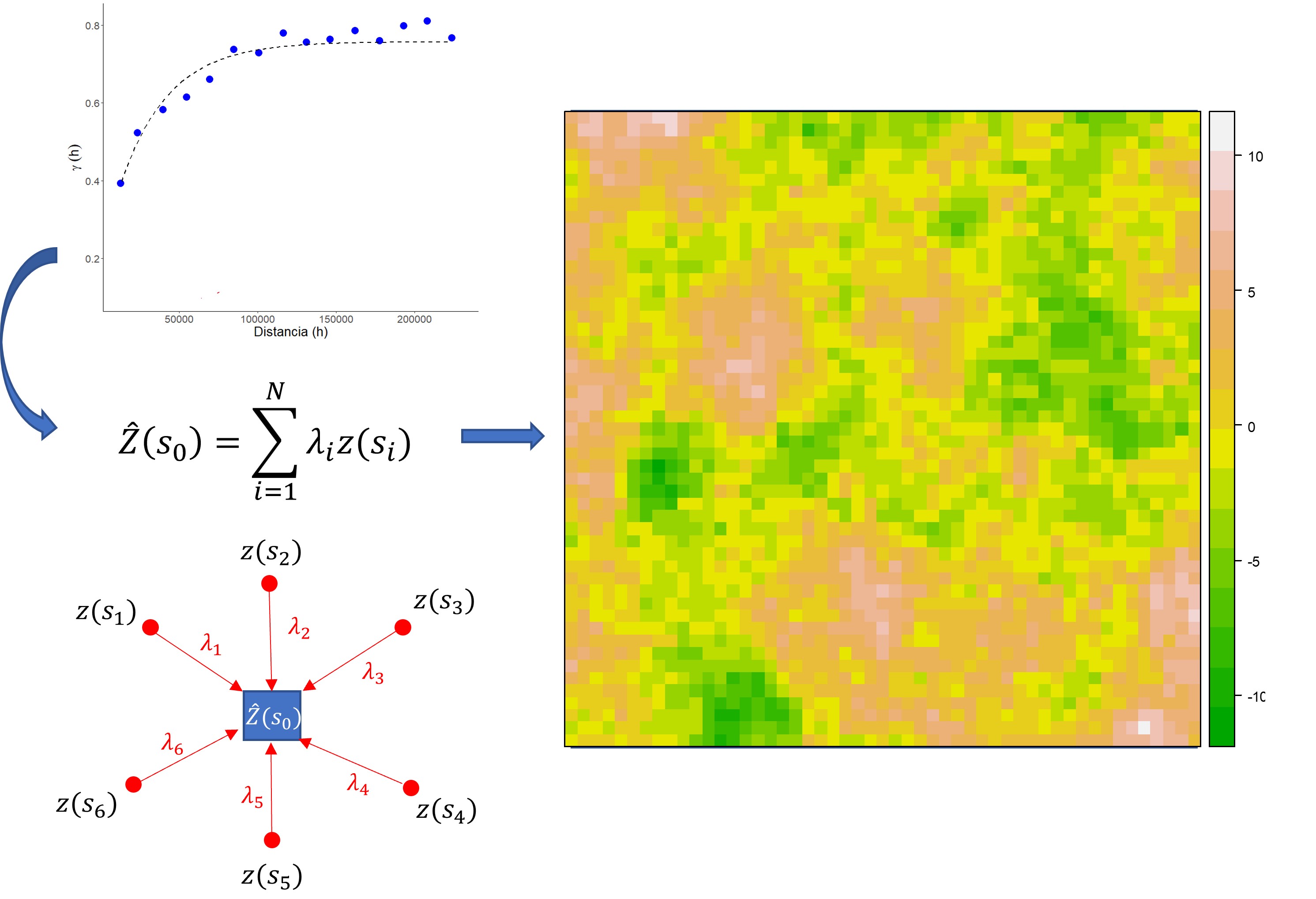
Kriging Regresión
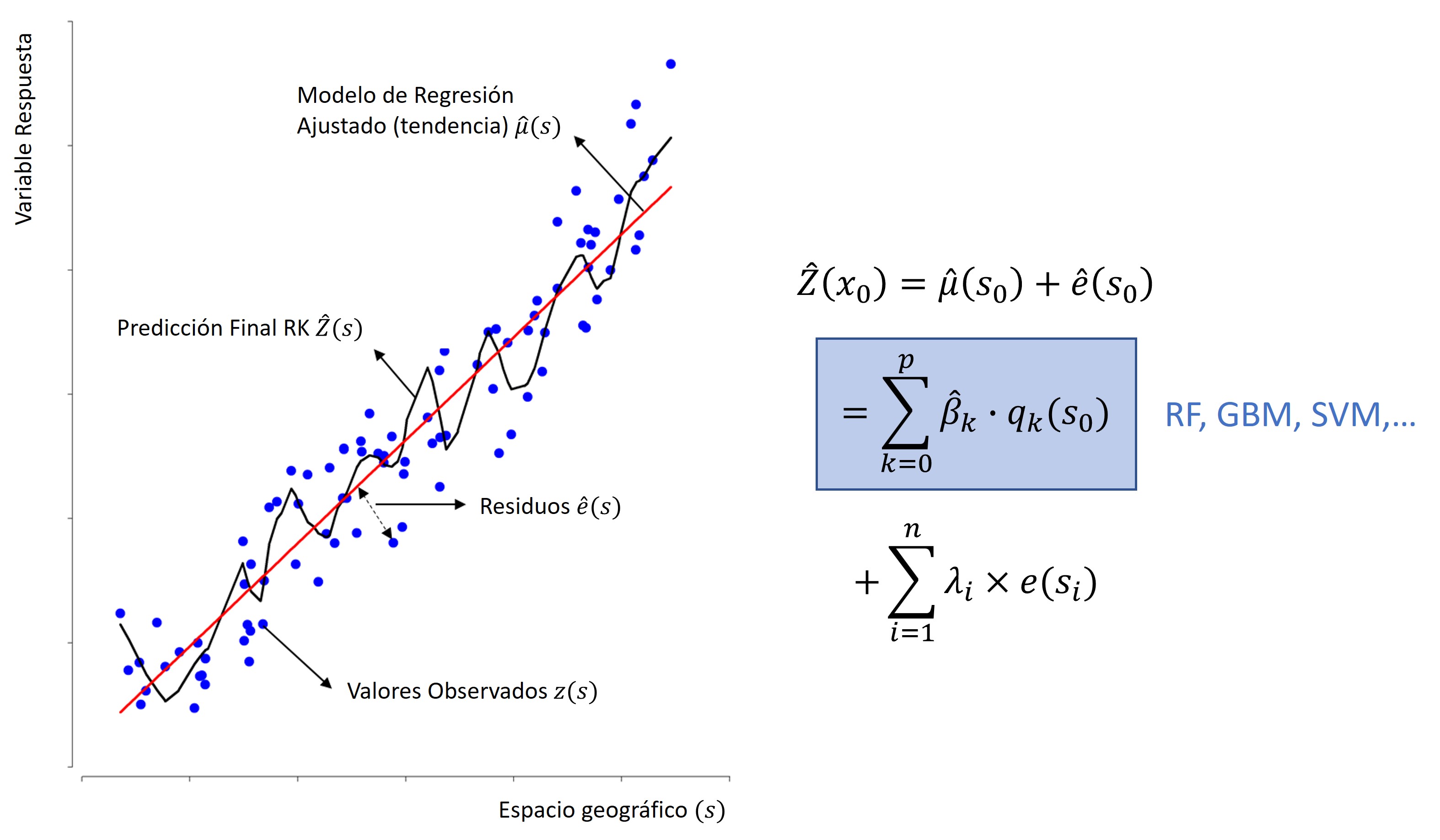
Interpolación Kriging
Kriging es considerado como el método de referencia para el análisis de datos geoestadísticos.
Toma un modelo estadístico integral como punto de partida y deriva en una predicción óptima.
Explota la autocorrelación espacial en la variable de interés.
Proporciona una medida espacialmente explícita de la incertidumbre de la predicción.
Puede ser computacionalmente exigente (tamaño muestra y grilla de predicción)
Requiere asumir supuestos estadísticos (estacionariedad, normalidad, relaciones lineales entre las variables involucradas)
No es adecuado para incorporar la abundancia de información de covariables disponibles en la actualidad.
Algoritmos de Aprendizaje Automático (AA)
En los últimos años, se produjo un incrementó en el uso de técnicas de AA para la interpolación espacial.
Estos métodos dependen en gran medida de la magnitud de la relación entre la variable dependiente y covariables
Una de las principales ventajas es su gran flexibilidad al incorporar diferentes tipos de covariables.
No tienen en cuenta que las observaciones están georreferenciadas y pueden estar correlacionadas espacialmente.
La autocorrelación espacial de la variable respuesta es capturada completamente por las variables auxiliares.
Algoritmos de Aprendizaje Automático (AA)
Enfoques para incluir información espacial en el análisis a partir de covariables espaciales:
longitud y latitud
distancias a esquinas y al centro del área a interpolar desde los sitios de muestreo
distancia de buffer desde los sitios de muestreo
- valores de los sitios muestreados más cercanas a los sitios de predicción
Alternativas:
- AA + Kriging
- Random Forest geográficamente ponderado
Interpolación Espacial Random Forest
\[\hat{z}_{(s_0)} = f \big(x_{1} (s_{0}),\dots,x_m(s_0),z(s_1),d_1,z(s_2),d_2,z(s_3),d_3,\dots,z(s_n),d_n \big)\] Donde:
- \(x_i(s_0) (i = 1,\dots,m)\) representa las covariables en el sitio \(s_0\)
- \(s_i(s_0) (i = 1,\dots,n)\) es el valor de la \(i-ésima\) observación más cercana desde \(s_0\)
- \(d_i=|s_i-s_0|\)